
This work is licensed under a Creative Commons Attribution 4.0 International License that allows sharing, adapting, and remixing.
The preceding example, which compared a local sample to a population mean, is not a true experiment. It is an interesting comparison for local educators. We could not, however, make strong conclusions about whether a particular kind of instruction was effective or not.
For this next example we will do a true experiment. Let's say that there is a new method of math instruction that is believed to be superior to older methods of instruction. We will form two equivalent groups of students by randomly assigning them to different classes. The control group will get the older, standard method of instruction. The experimental group will get the new instructional method. Both groups will be measured on a standardized math test at the end of the semester. The results will be compared to see if the new method is effective.
In PSPP, we will need a variable that represents the math scores (dependent variable). A second categorical variable will be needed to code for which group each student is in, experimental or control. Here is what the data might look like in our example.
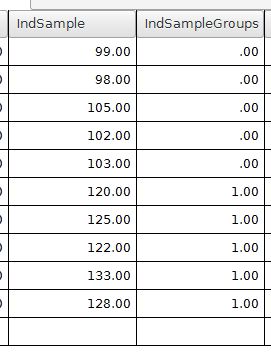
The variable IndSample is the dependent variable with the math test scores. The variable IndSampleGroups has a 0 or 1 coding scheme for representing the group membership. The 0 represents people in the control group. The 1 value is for people in the experimental group.
We will test for differences between the experimental group and the control group by using the independent-samples t-test. Choose the independent-samples t-test command by going to Analyze > Compare means > Independent Samples T Test.
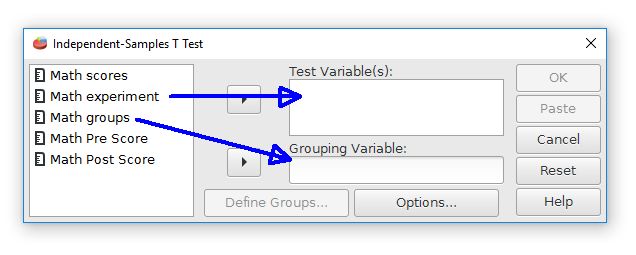
The first step is to choose the variables. Move the "math experiment" variable right to the Test Variable(s) field. This field is for the dependent variable. Move the "math groups" variable to the Grouping Variable field. This field represents the independent variable and group membership.
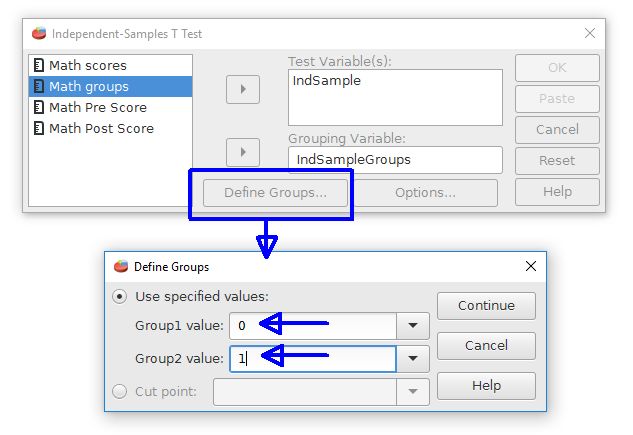
The second step is to inform PSPP how the groups are represented. Click on the Define Groups button. This opens a new dialog box. Enter the coding scheme values, which are 0 and 1 for our example. Note that PSPP has a feature for taking a continuously scaled variable and form two groups from a cutoff point if desired. This is represented by the "cut point" option.
Press the Continue and OK buttons to perform the analysis. The output will look like this:

The upper table shows some useful group statistics, like means and standard deviations.
The lower table has the t test results. This gets a little tricky because there are two versions of the test: Equal variances assumed and equal variances not assumed (see the rows). For most situations we will use the equal variances assumed version.
How can you tell which version to use? The Levene's test part of the output will give you the answer. When this test is nonsignificant use the equal variances assumed version. The Levene's test p value for this example is p = .259, so we will use the equal variances assumed version (marked in blue).
Our t-test result is t(8) = -9.20, p < .001 when expressed in APA style. We will reject the null hypothesis because this p value is less than .05. This is a statistically significant difference. The students who get the new math teaching approach are doing better than the students who received the older teaching approach.
Note that the p value (see Sig. 2-tailed) that PSPP gives is .000. Having a zero p value is not really possible, but PSPP can't make a judgment about something impossible. It would be best to report this result as p < .001 rather than p = .000.
A common mistake is to report the results from the Levene's test as being the t-test results. The Levene's test just helps us decide whether or not we need the equal variances assumed version of the independent-samples t-test. The Levene's test is not the actual t-test.
There are some other useful statistics on the right side of the table, such as confidence intervals, that are not shown on this page.

This work is licensed under a Creative Commons Attribution 4.0 International License that allows sharing, adapting, and remixing.